Shape #11: Cyclogon
They're the Shape of the Week
Take a square. Put a pen on its bottom left corner. Then roll the square to its right. Then roll it again. Then again. This traces out a shape called a cyclogon.

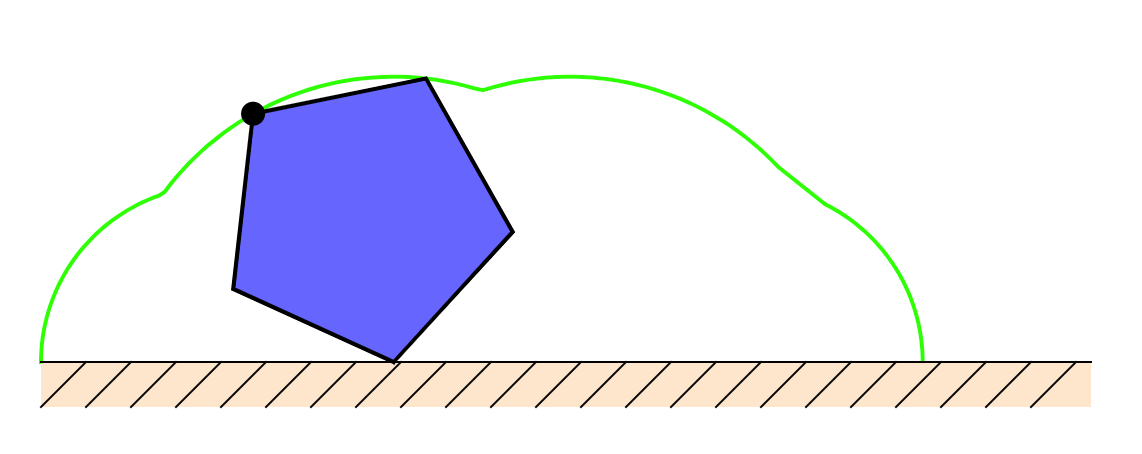
You can make a cyclogon out of any regular polygon. Just roll it along, and draw the curve traced out by a point. Here is a pentagonol cylcogon:
As far as I can tell, the cyclogon was named in 1999 by Tom Apostol and Mamikon A. Mnatsakanian. “When a regular polygon rolls without slipping along a straight line, a given vertex on its circumference traces out a curve we call a cyclogon.” Sure sounds like they’re laying claim to it.
Apostol and Mamikon have an interesting relationship. Mamikon was born in Armenia in 1942. He had an early interest in geometry but ended up getting a PhD in physics and becoming an expert in “radiative transfer theory,” which sounds cool but I know nothing about it. It has something to do with waves propagating through different mediums.
He ended up in California, applying his expertise to earthquakes, when the Soviet Union collapsed. He was stranded in California. According to Apostol, local mathematicians helped him navigate the immigration system and got him a stay as an “alien of extraordinary ability.”
Mamikon’s real passion was geometry and pedagogical visuals, and he came to Apostol with big ideas about ways of presenting algebraic and calculus ideas using dynamic visual representations. Apostol was blown away, and they wrote many papers and books together until 2016, when Apostol died at age 93. Mamikon passed away a few years later in 2021, at age 79.
Mamikon (I know it’s his first name, but Mnatsakanian is a mouthful) and Apostol have a clever formula for the area under a cyclogon. If you start with a regular pentagon, inscribe that pentagon in a circle—then the area of the cyclogon will be the Pentagon + (Circle x 2). And that’s not just true for pentagons, that’s true for any regular n-gon.
That’s very cool. And if you keep on adding sides you get something close (as close as you want) to a circle, and your cyclogon pretty much turns into a cycloid. And the area under that cycloid is exactly three times the circle, something typically proven with calculus.
OK, OK, but this isn’t the thing that I’m most excited by, and it’s not the thing that I want to show students. Instead check this out—draw the chords in those cyclogons, like this for the triangular cyclogon:
That makes a triangle whose area is exactly three times the original rolling triangle.
What if you draw in the chords of the square cyclogon? Then you get a trapezoid and its area is still three times the original.
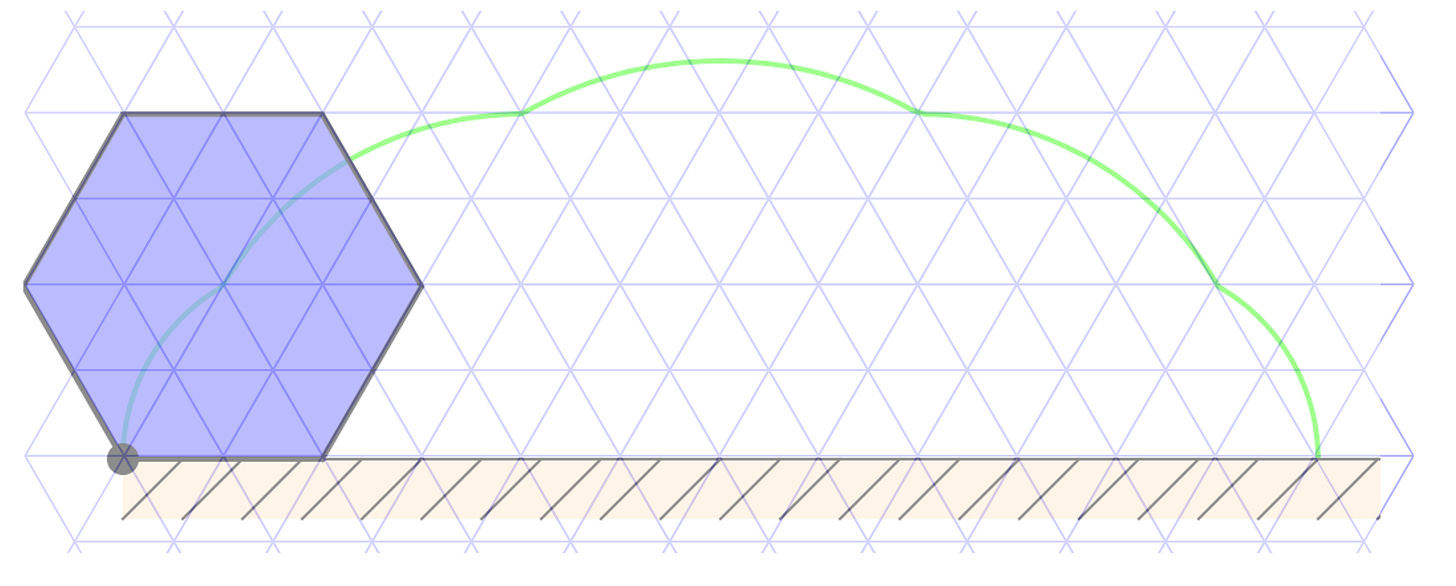
I’ve done my best here to impose the hexagonal cyclogon on a triangular grid, to make it easier to check the area. You could try drawing the chords yourself to confirm that the area is, once again, exactly three times the original polygon.
I mean that’s wild! But it’s true, and it’s always true for all regular polygons. There’s a paper from 1975 that calls these “polygonal arches generated by rolling a polygon,” but that’s because Mamikon and Apostol hadn’t yet named the cyclogon—now we can call these chord-cyclogons or something like that. And their area is always three times the original.
This is a good shape with a good name and some interesting math and I hereby declare it the shape of the week. Congrats to you, cyclogons. We will be back with more rolling shapes in weeks to come.
Classroom Ideas
How many arcs make a cyclogon? Is it always one less than the generating polygon—why?
Here is the chord-cyclogon generated by a triangle, square, hexagon. How many times bigger is the area than the generating shape? (Might be some fun, low-stakes discovery.)
Take a square, and try drawing the cyclogon. It’s kind of tricky!
What curve would you get if you didn’t start with a regular polygon? Would the area relationship with the chord-cyclogons still apply?
Be in touch if you have any further ideas of interesting things to do with cyclogons.







Love this. The joy of geometric relationships!