Making Things is Hard

My struggle with projects continues

I don’t know anything about Tamaki Seto, but in 2001 he invented Futoshiki puzzles. The rules are pretty simple. It uses the same grid logic as KenKen or Sudoku: if it’s a 5 x 5 grid, the numbers are 1 through 5. Each number appears once in every row and column.

Apparently in Japanese, “futoshiki” means “inequality.” Makes sense—besides for the grid, the only other hints are inequality signs.

You might want to try to solve these things. They’re fun, you should! But how do you make your own?

I made a blank template to experiment. I tried putting in a few numbers and inequalities and seeing if I could make it work. I gave it to my students (who are in a puzzle-y math elective). It quickly became clear that they weren’t making much progress. At all. And neither was I.

Some people, when they get stuck on something, work harder. Well, that’s not me.

I went searching for someone who had already figured this out and found a paper titled “The number of inequality signs in the design of Futoshiki puzzle.” I don’t really understand it. But the author describes a procedure for creating Futoshiki puzzles, that roughly goes like this:

• Randomly fill the grid with numbers that have no repeats in rows and columns (i.e. make a Latin Square).

• Fill it with inequalities, to the max.

• Then delete something randomly, either a number of an inequality.

• Make sure you can still use logic to derive the missing info.

• Then randomly delete something else.

If you reach a point where you delete something that makes the puzzle impossible to solve…don’t do that. Put that info back in, and then, blammo. You’ve got your puzzle.

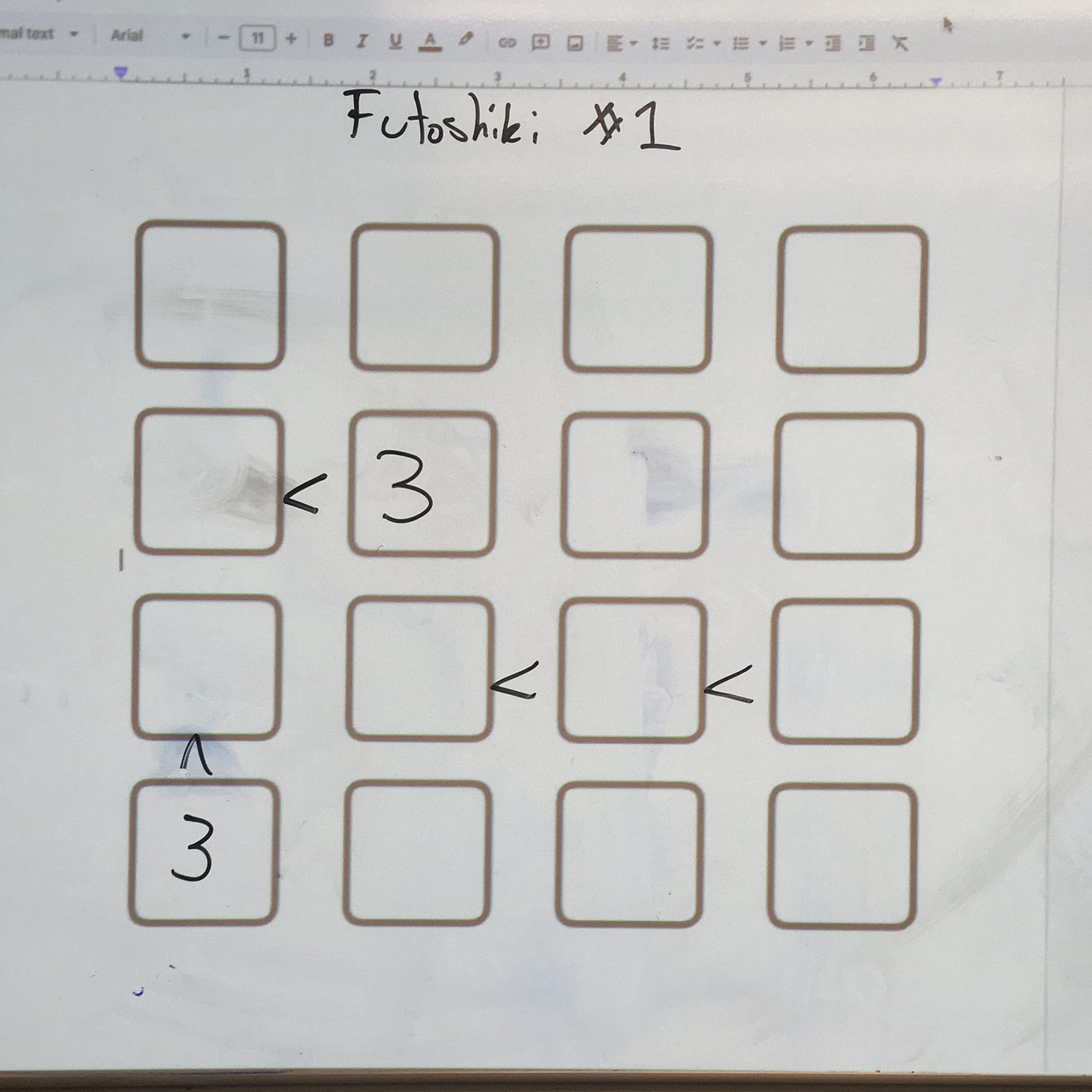
When I shared this with my students, I led them at the board in making a Futoshiki. Here is what we came up with:

But it’s surprisingly frustrating process!

With all the deleting, I’m 95% sure that this solvable but I have no clue how difficult it is. If you told me to make one that was more (or less) tricky, I’d have no clue how to do it.

And it’s also tedious. Creating puzzles in this fashion requires solving and resolving the puzzle. You have to check carefully to make sure you don’t go too far. It’s like solving the easily possible Futoshiki over, and over, and over again.

And it’s a shame that creating puzzles is so tedious and unpredictable, because my students loved having a puzzle of their own creation. There was delight at the idea that we might stump others with this thing. People wanted copies to take home, to share with siblings, etc.

For the past few years I’ve told myself, at the start of the year, this time I’ll have students do more projects. How many? Not many! Just a few. I’d love for them to feel proud of something of their own creation.

But then I get a bright idea—try making your own puzzles! And the experience is frustrating, disappointing. Or at least enough of those things that it doesn’t check the emotional boxes that I was aiming for in the first place.

Looking back, though, the most fun we had was at the board, making these together. I was leading the process, taking suggestions, basically conducting the operation. And the process was interesting, and everyone had a puzzle that they contributed to.

There are tradeoffs here. This could work fine in my elective, which only has a few students. It would work less well in classes with twenty students. And how long can everyone really pay attention to the same discussion? Will everyone really feel part of this effort?

But maybe there’s a way to keep it manageable. That’s my resolution, then: I’ll try to tell the class that we’re going to make something, and that we’re going to make it together. A whole-group project, if that even makes any sense at all.