Shape #3: Salinon
Congrats, salinons.
This is a salinon, and it is the shape of the week.
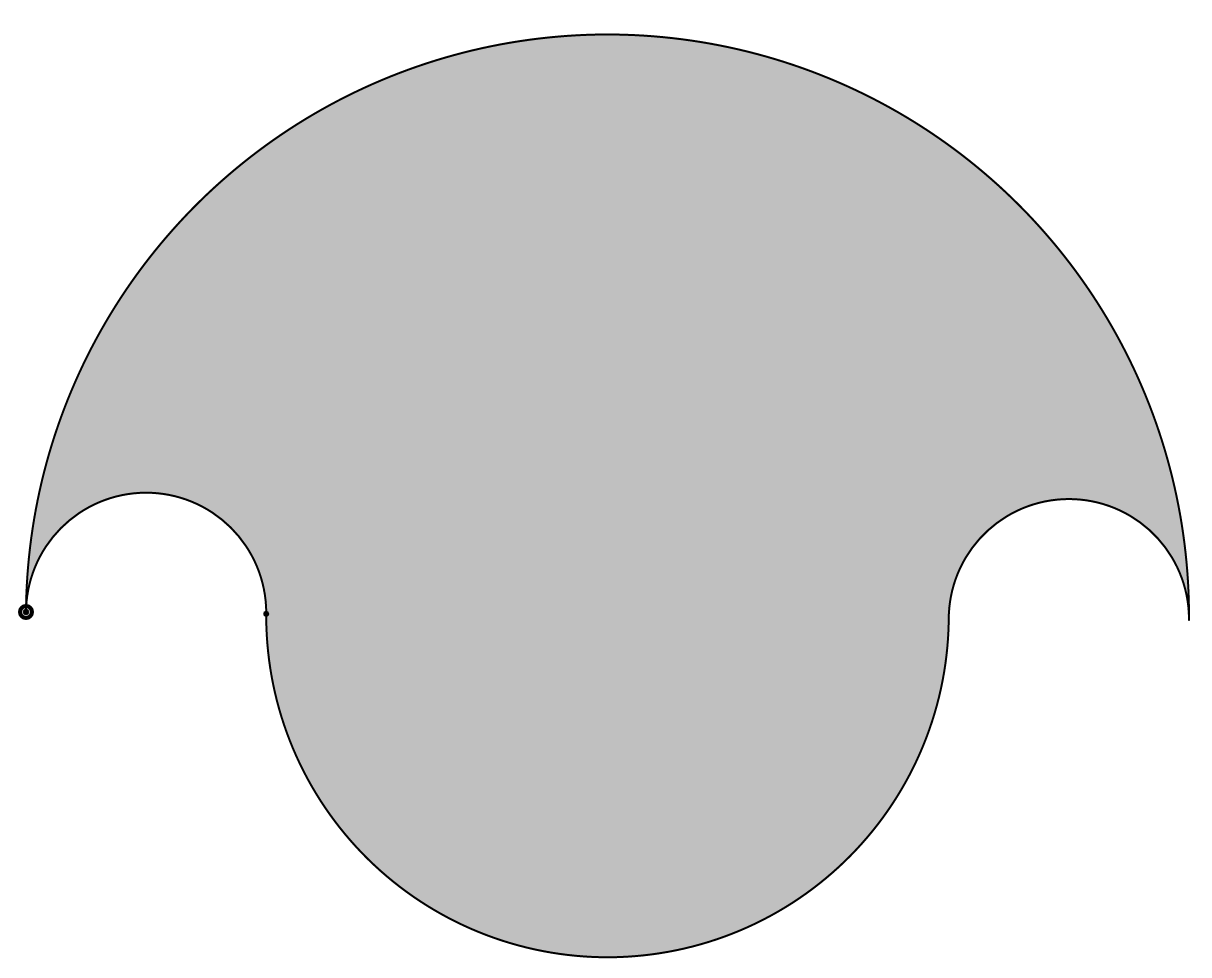
Salinons are made from four semicircles, but always constructed in a particular way. I can’t find a nice way to describe it in words: it’s always one large semicircle with two smaller identical semicircles cut out on each side, with a semicircle between them on the other side of the diameter.
Incomprehensible, right? But here are a bunch pictures that get the point across more clearly:

If you start playing with this dynamically, it’s hard to resist bringing those two circles together until they meet at a point. That creates an arbelos. And what if you keep going? That creates a weird criss-cross pattern and I’m no longer sure what we call that, but it sure is pretty.
Salinon means “salt cellar” in Ancient Greek, and I immediately had visions of a huge basement piled with mountains of crystal-white salt, but no apparently this is badly wrong, apparently it’s a bowl? The images I could find online look nothing like the shapes so I really have no clue where the names comes from, but there you have it.

Now, on to the theorems. Salinons have an area formula!
Here’s my little derivation. It’s nice! (And though I haven’t checked, it sure would be fun if it were true for that weird crossing salinon with the weird criss-crosses above).
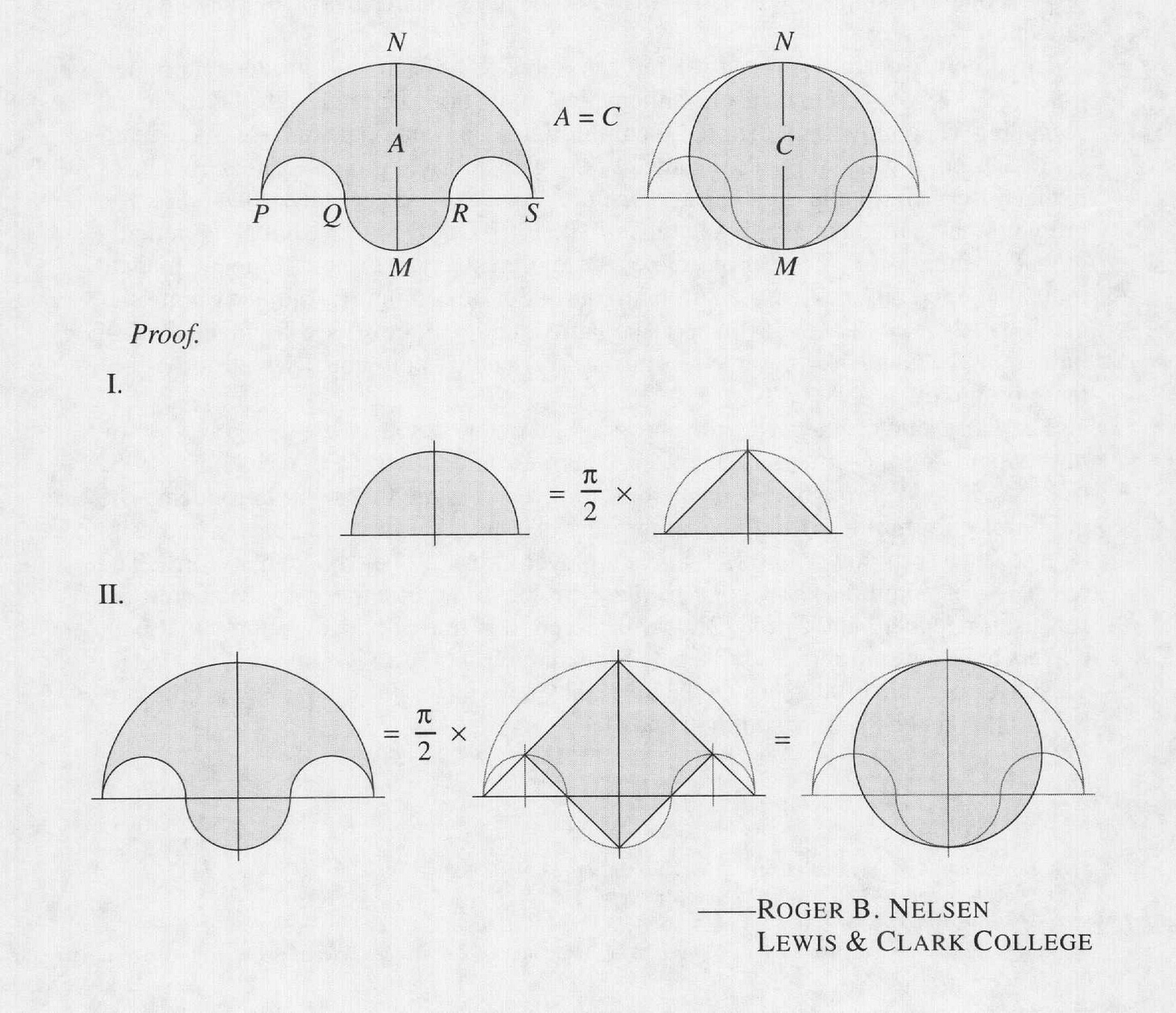
There is one more cool thing about this salinon, and from what I can gather it’s the salinon’s claim to fame. Draw a line from the tippy-top of the salinon to its very bottom. Draw a circle with that line as the diameter. It ends up looking like this, with a big circle on top of the salinon:
Theorem, found in Archimedes: the circle and the salinon always have the same area. (I think you can prove this using the area formula derived above, as that circle’s radius is half of r_1 + r_2.)
When I went searching around for info about the salinon, I found a “Proof Without Words” for this Archimedean idea but, honestly? I don’t like proofs without words. Just tell me what the pictures mean! Anyway, here it is, after staring at it for a while I think I could explain but honestly my ability to articulate the proof comes and goes.
I shared this with my brilliant geometry-teaching colleague, and credit goes to him for making an amazing observation. What happens if you replace the semicircles with four other shapes?
You may be familiar with the crux of this idea from the Pythagorean Theorem. Swap out the squares on each side of the right triangle for equilateral triangles, rectangles, semicircles and the relationship still holds—as long as the three shapes are similar, the area relationship is exactly the same as it is for squares.
So, what if you did that for the salinon? Replace each semicircle with a rectangle, an equilateral triangle, or a square. Would the Archimedean relationship from above still hold?
I think we’ve convinced ourselves of an answer, and we think that answer is “yes.” Congratulations to salinons, this week’s shape of the week.
UPDATE: Yes, you should really go ahead and find a formula for the perimeter of a salinon. I did this in class and it went quite well, though it does involve a tiny bit of algebra.
If you care for spoilers, then note that if the long diameter is x and the short diameter is y, then the diameter of the whole thing is pi*x/2 + pi*y/2 + pi(x - y)/2…add those together, and that’s all you need to know!