Shape #1: Zonogon

A new feature

Let’s name all the shapes a person encounters in 13 years of schooling:

• triangles (right, isosceles, obtuse, acute, equilateral)

• quadrilaterals (rectangle, square, parallelogram, kite, trapezoid, rhombus, maybe arrowhead)

• circles

• polygons (regular and not)

• pentagons, hexagons, septagons, octagons, etc., just long enough to name them

That’s a pretty great collection of shapes. But I have to admit, after thirteen years of teaching this stuff, I’m a bit bored. So in my high school geometry class I have been trying to make “Shape of the Week” a thing, mostly for selfish reasons—to expand my own geometric pallette.

But the kids seem to be tolerating it so far. (I think we’re on Week 6.) What we do is, I introduce the new shape at the start of the week, briefly scroll through wikipedia and show them any cool things. Then, if I get excited by anything, I turn it into a brief activity or warmup. I don’t know if this is good teaching, but it’s fun.

Then I thought, hey, maybe you’d all like this. So, let’s do it: the shape of the week is the zonogon.

THE ZONOGON (from wikipedia)

A zonogon is like a parallelogram—opposite sides are congruent and parallel. But it’s also important to notice that it has point symmetry. In other words, you can spin it around a center and (halfway through the turn) you get what you started with.

Also from wikipedia.

Now, for some fun. Go ahead and draw lines until these hexagonal zonogons are carved up into a bunch of parallelograms. Go ahead, I’ll wait…

SOLUTIONS TIME:

Sorry for the sloppiness, I drew these on the computer.

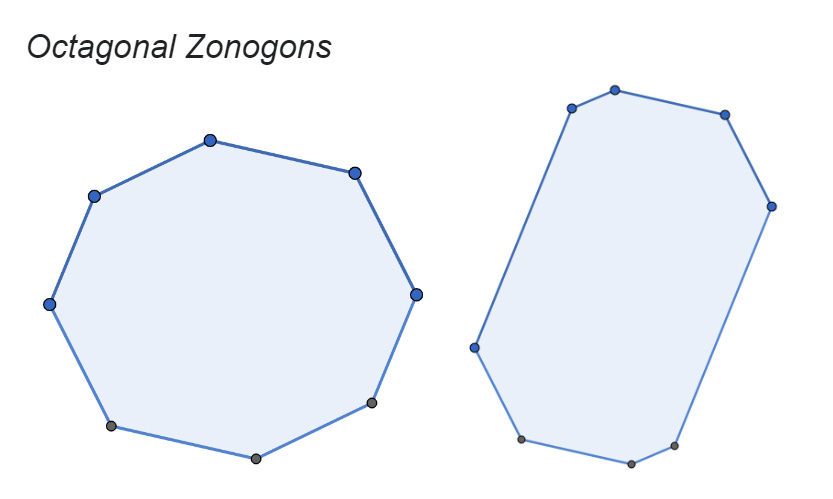
Well now, three parallelograms each! How many parallelograms do you predict an octagonal zonogon can be broken into?

Here are some octagons, go and find out (I’ll wait):

Answers below!

It’s 6. I’m having fun! Hope you are too. Here are some decagonal zonogons.

And, good news, they can be broken into 10 parallelograms. So here is our number sequence: 3, 6, 10,…

Do you recognize this sequence? You might! It’s the triangular numbers: 1 + 2, 1 + 2 + 3, 1 + 2 + 3 + 4, and so on.

Of course, wikipedia.

There are a lot of things I don’t know about zonogons. For example, how many different ways are there to do this parallelogram dissection? I don’t know. But I do know that when these zonogons are regular, the parallelograms become rhombuses and we get GORGEOUS dissections. Check out this, from the late great Don Steward:

What are those angle measures?

Anyway, I’m glad to know about zonogons. There is something called Minkowski’s First Theorem in the Geometry of Numbers (this YouTube video helped me understand it better) and in the 2D case it involves zonogons. That’s it’s own interesting little thread to chase—it tells you how big your zonogon can get if its vertices are on the grid before it contains one of the grid points in its interior.

So, congratulations to zonogons! Enjoy your time as shape of the week. If this stays fun, I’ll be back in your inbox with a new shape soon enough. Bye now!