Shape #9: Reuleaux triangle

Shape of the Week is back.

I.

Franz Reuleaux (1829 - 1905) was an engineer. His father and grandfather were machinists, and after some work in the family business he became a university professor and theorist of the mechanical age.

The 19th century featured an explosion of machines and inventions. You know how smartphones changed everything? Commercial train travel emerged in the 1830s. Samuel Morse sent the first telegraph—“What hath God wrought”—in 1844. The tin can was invented in 1810. The world might be changing fast now, but the 19th century was insane.

Reuleaux was one of the theorists who arrived to try to make sense of this new world, to produce useful ways to think about it. This is theoretical work, but theory is often close to pedagogy, and for teaching purposes, Reauleaux made a lot of physical models. Today they’re mostly housed in Cornell University.

One of these weird little models was a three-cornered shape encassed in a square chamber. It could move freely inside it, and actually could rotate cleanly inside that square. This is of course now known as the Reuleaux triangle, and it’s the shape of the week. (Sorry for the break in posts, but SoTW is back, baby.)

The Reuleaux triangle is not a circle, but it’s a bit like a circle. If you stick a circle in between two planes, the planes roll nicely. Reuleaux’s triangle does that too.

These shapes are said to have “constant width”—there are obviously some parts of the “triangle” that are wider than others, but if you roll it between those two planks, its width between the contact points perpendicular to the planks will always be the same. Just like the diameter of a circle.

Mathematicians love the Reuleaux triangle. It’s one of those things—Martin Gardner wrote about and helped popularize them. You can make fun rolly-models of the shape, and it’s genuinely surprising that they work as smoothly as they do. It’s often trotted out as a cool bit of math because it is, in fact, very cool.

You make a Reuleaux triangle by starting with an equilateral triangle. Then, draw a circular arc centered on one of the triangle’s points, passing through the other two points. In fact, do this with other shapes too, not just equilateral triangles. Then you get Reuleaux polygons.

From BEAM

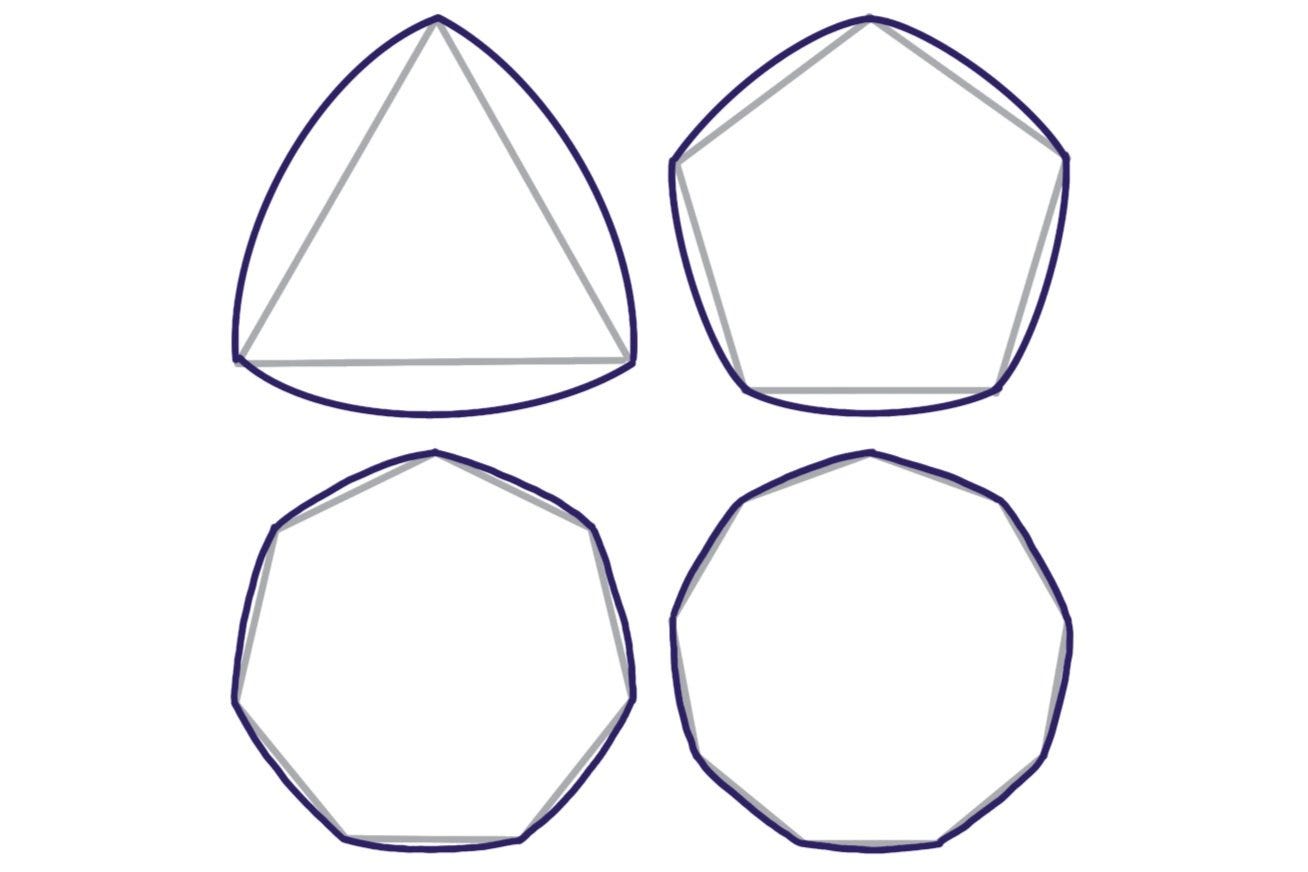
(Hey—notice that these all have an odd number of vertices? That’s not an accident, you can’t really make these things if there are an even number. Try it with a square, and you’ll see the problem.)

II.

Now, there is a theorem about these shapes, maybe you know it already, maybe you don’t, but it’s a real good one.

START with a circle of radius 1 unit, that rolls nicely between two planks spaced 2 units apart. It has a circumference of 2pi units. That’s a formula we teach kids in middle school, diameter times pi.

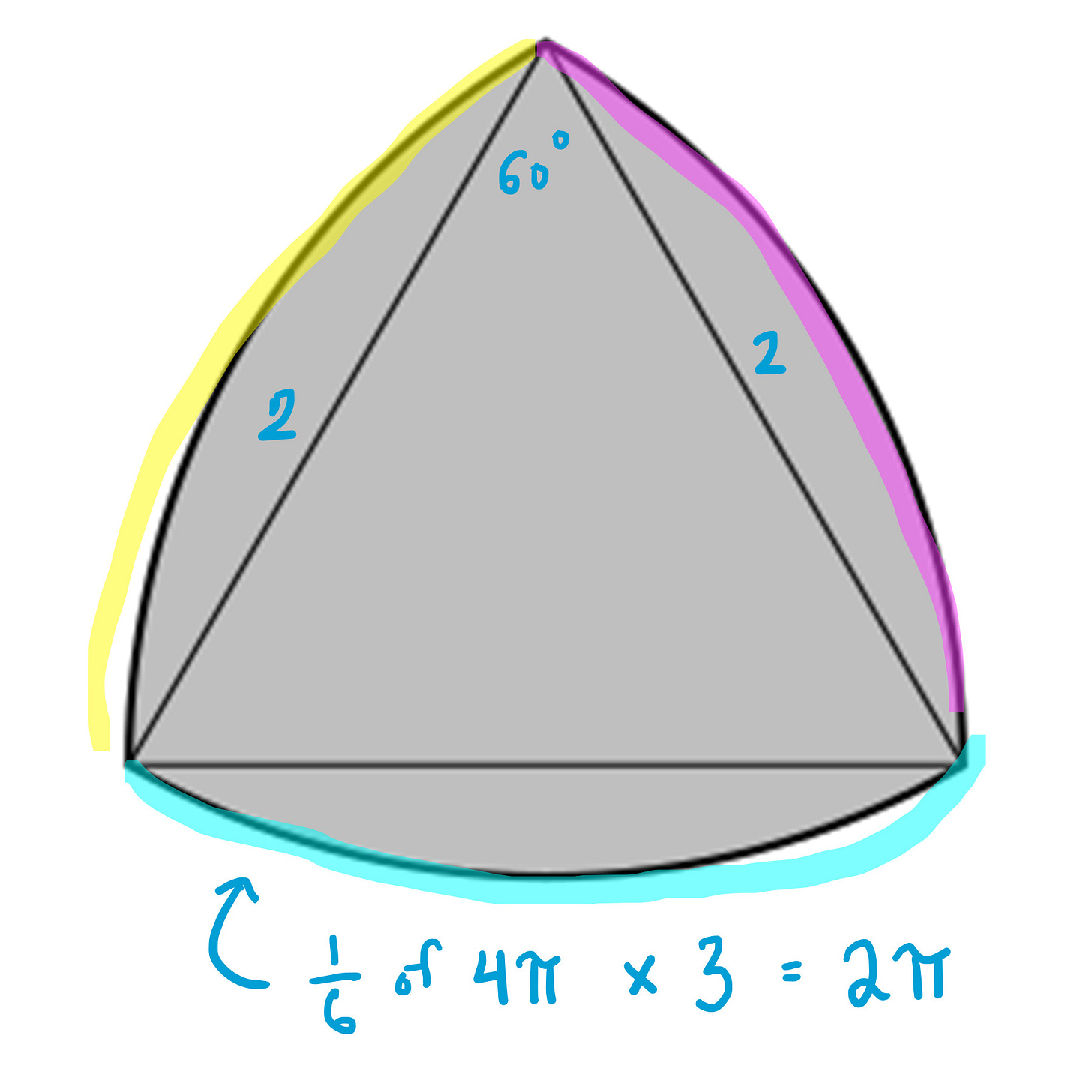
NOW let’s find the perimeter of the Reuleaux triangle. Its made of three circular arcs. Each arc is a sixth of a circle’s perimeter. And, because this has to roll between those two planks spaced 2 units apart, those circular arcs have radius 2. That’s three times a sixth of 4pi, or 2pi. A picture is probably clearer.

AGAIN consider the Reuleaux pentagon. It has five arcs, and though requires a bit of angle work, each arc is a tenth of a circle’s perimeter. The arcs still have a radius of 2 units, so that’s 5 times a tenth of 4pi, or 2pi.

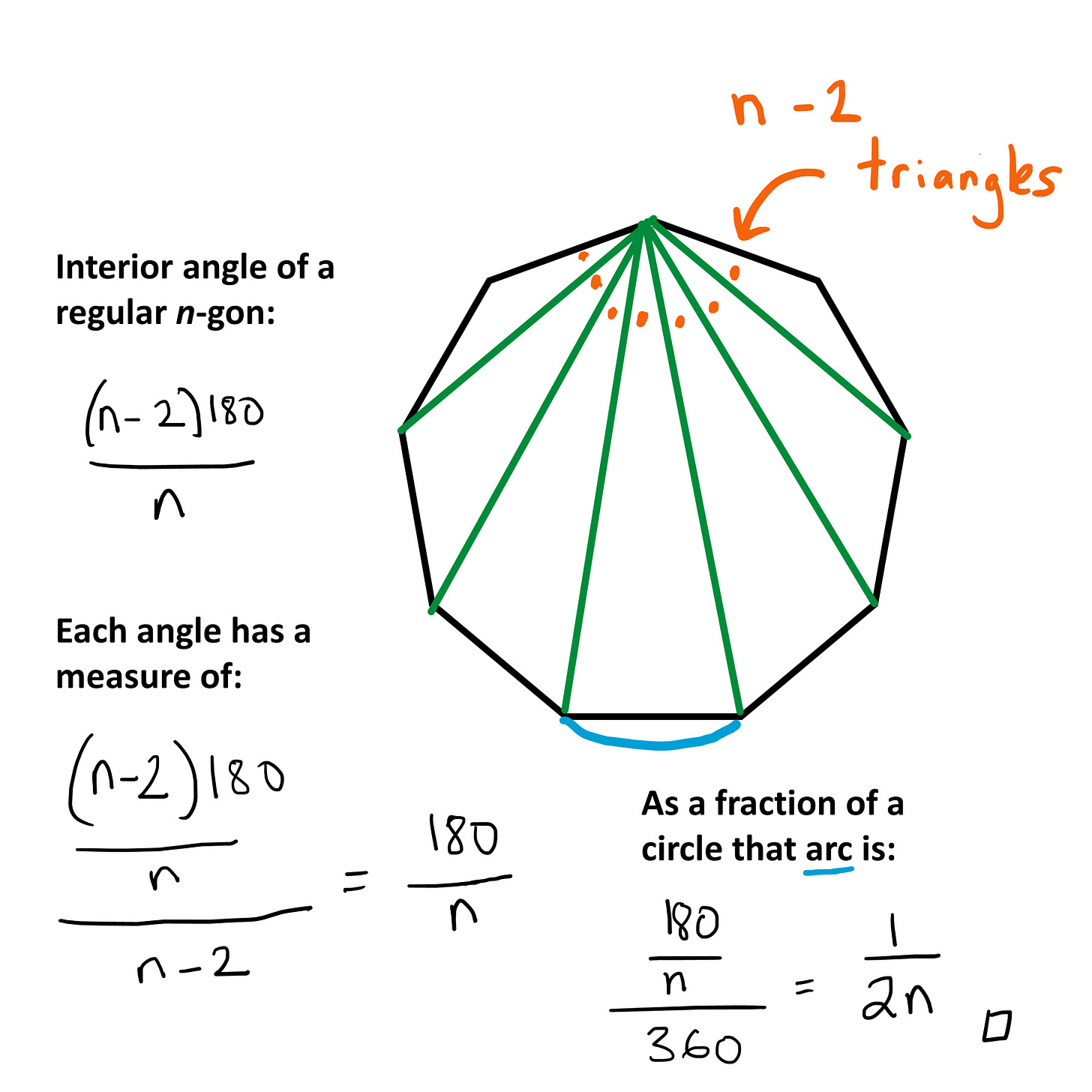
SEE WHERE WE’RE GOING? The Reuleaux n-gon will have n arcs. The radius of each arc will still be 2 units. We just need to be sure that each arc will always be 1/(2n) of the circle’s perimeter…

Here’s a proof of that, using something called the fan triangulation:

Thank you to Benjamin Leis for pointing this out to me.

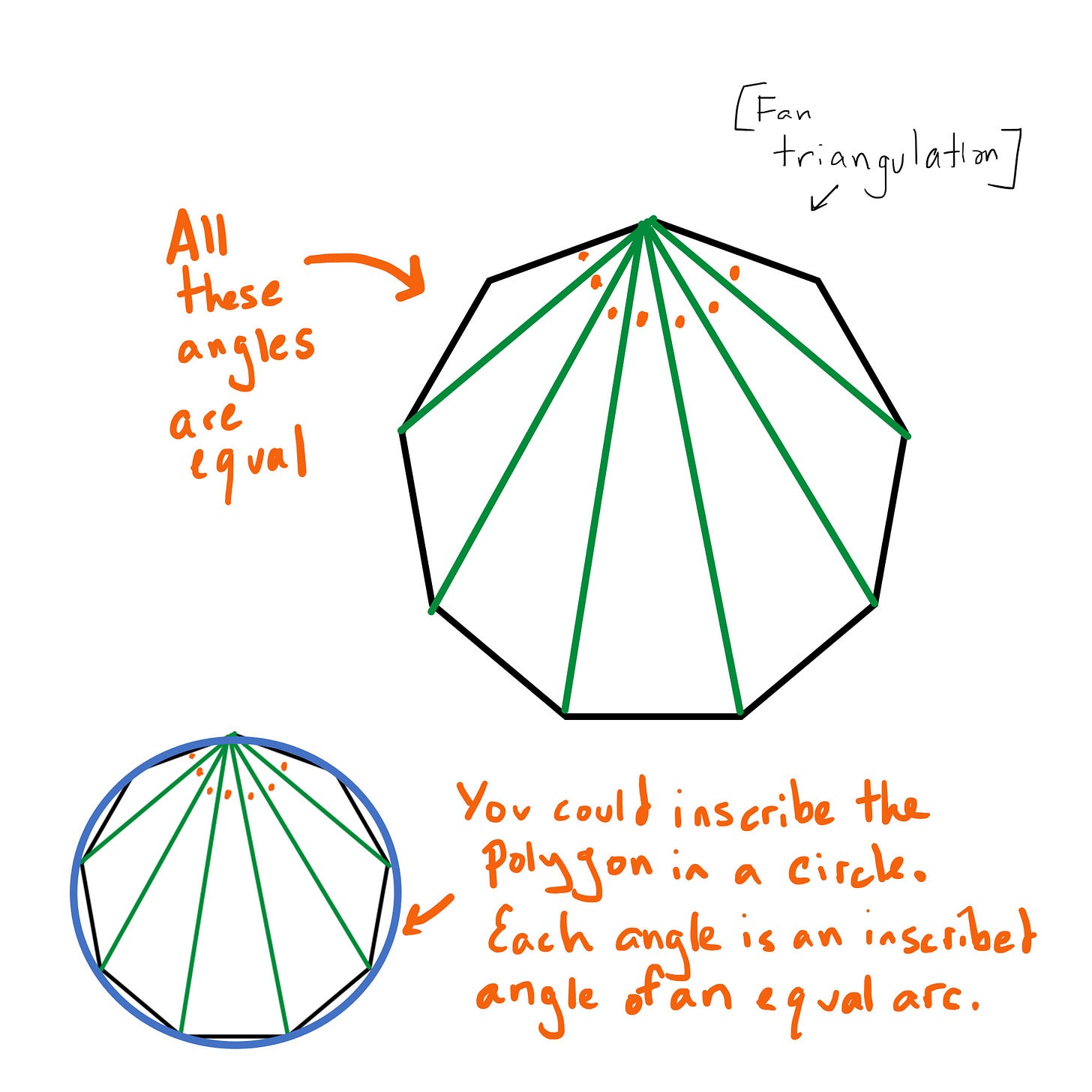
It works! And therefore: Every (regular) Reuleaux polygon has the same perimeter as the circle whose width it shares, i.e. width times pi.

It’s the same as the circle—fantastic!

III.

It goes further, because it’s not just these regular polygons, but any shape of constant width. That is, every shape of constant width has the same perimeter formula.

This is Barbier’s theorem. If you’re dying to see some of these non-regular shapes, check out wikipedia.

Credit to Jonathan Spiegelglas for creating the clearest, coolest explanation of a proof of this theorem that I’ve seen. It uses something called Minkowski sums, basically a sort of dragging of a shape through the interior of some other shape, it makes more sense when you put it in action as Speigelglas has shown:

Credit to Jonathan!

I’ll send you over to Jonathan’s post for the full explanation. I’ll link to the wikipedia article for Bodies of Constant Brightness, a gorgeous phrase that will someday be the title of a lovely book of poetry and is a 3D analogue to Barbier that I don’t yet understand.

And that’s all I know about Reuleaux triangles, the work of a machinist and engineer that mathematicians have lovingly borrowed for years and years.

---

Questions that might be good to ask students:

• Where is the constant width—isn’t it narrower on one end?

• What are some similarities between Reuleaux triangles and circles?

• How can you construct a Reuleaux triangle, pentagon, and septagon?

• Try to construct a Reuleaux square. What goes wrong?

• Find the perimeter of the Reuleaux triangle.

• Find the angles in a regular pentagon that has been fan triangulized.

• Find the perimeter of the Reuleaux (regular) pentagon.

• Find the perimeter of the Reuleaux (regular) 99-gon.