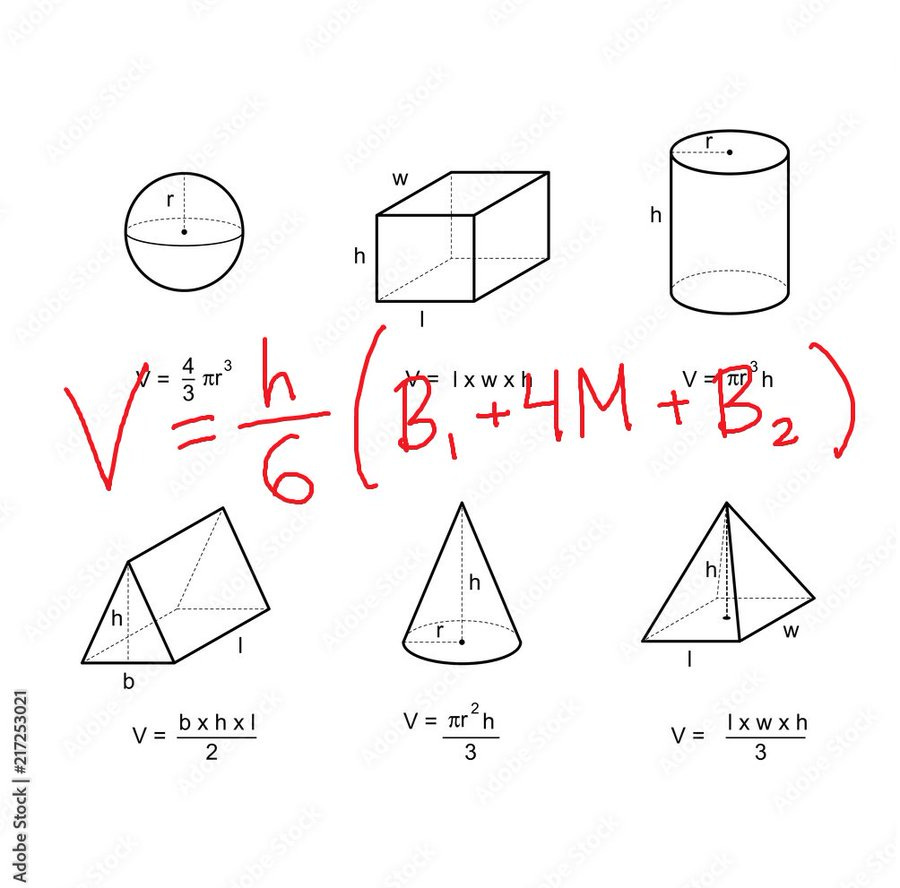I am so into prismatoids right now! I can explain why they are so cool, but it’ll take a minute of your time. BUT I PROMISE IT’S WORTH IT.
OK, what are we talking about here? Prismatoids. A cube is a prismatoid; a prism is a prismatoid; so is a pyramid; a frustum; an antiprism and a cupola, both former shapes of the week, are prismatoids. (Prismatoids, it goes without saying, are the shape of the week.)
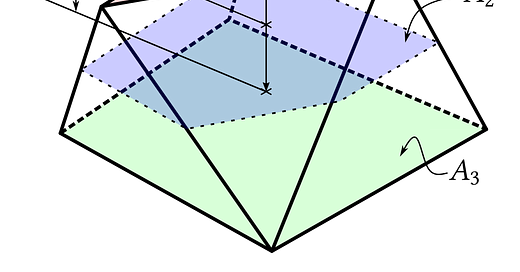
All these things are prismatoids, because a prismatoid is a polyhedron whose vertices all lie in two parallel planes.

Still with me? We’re now going to talk about volume.
The volume of a prism (or a cylinder) is the area of its base times its height:
The volume of a pryamid (or a cone) is a third of the prism (or cylinder) that contains it:
NOW: what if I told you that there is a single volume formula that applies to both these prismatoids, PLUS the other ones whose volumes are much harder to find?
GOOD NEWS! The volume of a prismatoid is
where the Bs are the bases and the M is the area of the middle cross-section, exactly halfway up the height.
CHECK IT OUT: all the other volume formulas pop out of this one. For a prism, the Bs and the M are all equal:
And for pyramids, the top base has area zero, and the middle slice (whose sides are scaled down by 2) has a quarter of that area:
OK, so far so good. We’ve got a single formula that works for prisms, pyramids, (and by extension) cylinders and cones.
What if I told you that you could think of a sphere as a kind of generalized prismatoid? BECAUSE YOU CAN!
The sphere’s top base? Area of zero. Bottom base? Area of zero. Middle section? Area of a circle. Height? A diameter. Now, watch:
HOT DAMN!
And that’s not it. This one single volume formula works for ellipsoids, spheroids, and wedges, even weird non-polyhedral ones like the blobby knife shown below:
If you’re looking for more, I highly recommend this 1952 Mathematics Teacher article, “Some Notes on the Prismoidal Formula.” There are limitations on when this formula works for blobby things, and the reasons have to do with calculus. (If you teach calculus, you might want to take a look at this! It would make a great exploration.)1
And if you’re looking for a proof for the polyhedral prismatoid, you can play around with this Geogebra sketch that someone made. You prove the formula by picking a point in the middle slice and splitting the prismatoid up into a ton of pyramids.
I find it absolutely wild that this these are not more widely known, but prismatoids are delightful so let’s get out there folks and spread the word!
Addendum
The end of that Mathematics Teacher paper has an advertisement for a geometry exhibit in Chicago’s Museum of Science and Industry. To accompany it they announce the publication of a pamphlet with the mildly threatening title “You Will Like Geometry”:
Chicago's Museum of Science and Industry announces a new exhibit on geometry which should be of interest not only to teachers and students in the Chicago area but to those who will be visiting there in the forthcoming months. The exhibit presents geometry as being "amazing, ingenious, beautiful and profound" and was designed by Dr. Karl Menger, professor of mathematics at the Illinois Institute of Technology. A pamphlet describing some of the material shown in the exhibit entitled "You Will Like Geometry" may be purchased at the Museum for 10 cents or will be mailed from the Book Mart of the Museum if the order is accompanied by 13 cents in stamps or coin
Well, I had to see this! Jesse Fuchs helped me out, and the opening pages did not dissapoint:
This was written by Karl Menger, who also wrote a piece titled “Why Johnny Hates Math” for Mathematics Teacher. I think Menger’s answer is that Johnny hates that teachers aren’t sufficiently precise, and he recommends that extreme care is used by e.g. using three different fonts for different uses of variables? Wild stuff, when all Johnny really wants is to mess around with prismatoids.
Define a function f(h) that takes “distance h from the top of the shape” as an input, and have “area of a cross-section at distance h” be the output. This formula will work if f(h) is a cubic, quadratic, linear, or constant function. I have no intuition for this whatsoever beyond the calculus proof shown in that paper.