Ayn Rand, author of Atlas Shrugged and other books about robust individualism, had a favorite painting. By her own account, she would spend hours at the Museum of Modern Art standing in front of Salvador Dalí’s Crucifixion (Corpus Hypercubus), gazing upon it. Whatever you think about Rand, can you blame her? It’s an image worthy of attention.
The painting has something to do with what Dalí called “nuclear mysticism,” an attempted fusion between science and religion. That sounds a bit like the “anthrosophy” that inspired Paul Schatz to invent the oloid, a shape previously covered in these pages. There is something about mysticism and geometry that goes back to Plato, back to Ezekiel, probably much farther.
“Levitating before a hypercube—a geometric, multidimensional form—Christ’s body is healthy, athletic, and bears no signs of torture,” says the note on the MET’s website. But, technically speaking, this is not a hypercube but rathers the unfolding of a hypercube, i.e. its net.
The net of a cube is also a cross. Geometrically, you could call it a polyomino—a six-squared domino. But Dalí’s net is a 3D polycube, so you have to imagine it being folded up into a 4D shape, and before you ask—no, I don’t understand this at all. But let’s not let that get in the way of a good time.
In the language of polycubes, Dalí’s cross is an octacube, one of 3811 ways of putting eight cubes together face to face. Apparently, just 2611 of these can be folded up into that tesseract, the 4D cube.
Now, I know what you’re wondering: if you packed these octacubes in a particularly clever way, could you fill all of space with them? (What is with the mathematical obsession with filling space, anyway?) The answer comes in a 2015 paper by Giovanna Diaz and Joseph O’Rourqe, and the answer is yes.
Their argument involves laying the crosses side by side to create sheets of octacubes. They then stack those sheets, showing that the “bumps and dents” fit together perfectly with four stacks, like an unending plane of dead bolts. This, they argue, regains the original sheet’s pattern, enabling them to continue filling space with these octacubes indefinitely in every direction, forever.
Now, we might wonder whether we can unfold the 3D cross itself. Can a 2D net of the 3D cross be created? Can you make a polyomino out of it? Once again, the answer is yes, yes, yes.
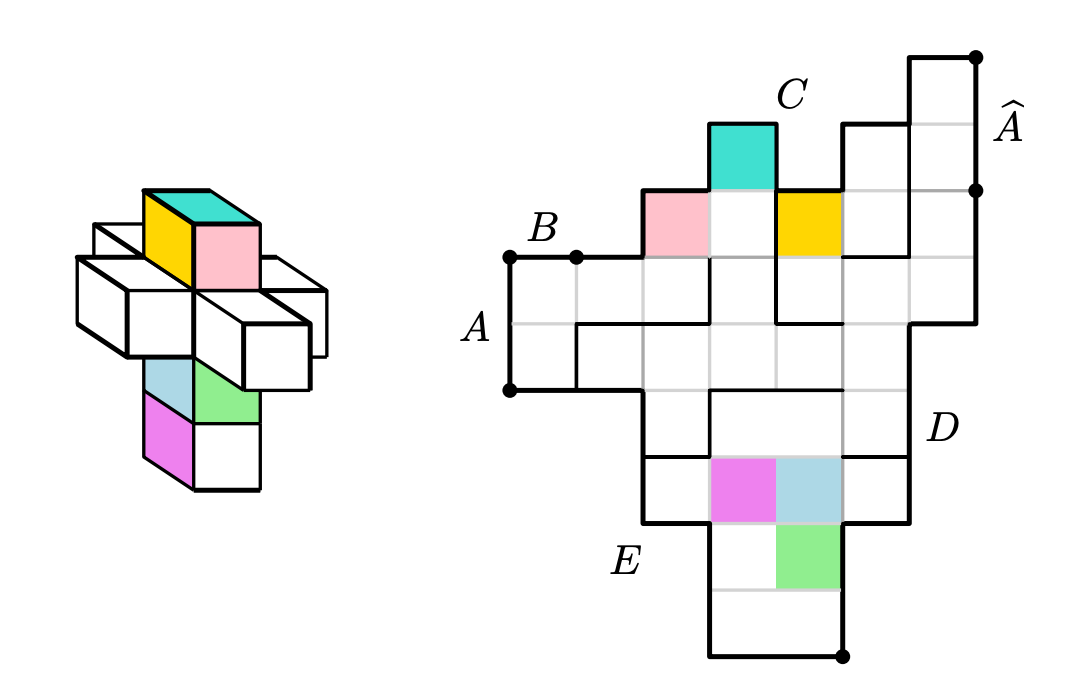
Not only can the cross be unfolded to a polyomino, but you can tile these nets themselves forever and ever and completely cover any surface—the face of a hockey rink, a smooth court, or some infinitely flat planet. The unfolding of the unfolding of the hypercube itself fills 2D space completely.
That this can be done shouldn’t be taken lightly, as not every 3D polyhedron can even be unfolded. In fact, there are many, many polyhedra that have no net whatsoever—no unfolding that preserves all its edges.
Which leaves us with a question: can every polycube be unfolded to a polyomino? The question is open—nobody knows the answer. It remains completely unknown, currently beyond the grasp of humanity, hidden behind some mystical veil…or maybe it’ll be proved in like a month, I honestly don’t know. Anyway, that’s the polycube, the shape of the week.
Questions You or I Might Ask Students To Think About
How many polycubes can you make with 4 cubes? Would 3D tetris work with them?
What’s the polycube with 3 cubes of least surface area? Of 4 cubes? Of 5?
Check out the Soma cube…how many ways can you find to put those polycubes together to make a 3 x 3 x 3 cube?
Note: 261 in Hebrew gematria, a secret letter code, is the value of A.S.R., or asar, which means to bind. It also is the value of N.H.O.R., nahor—light. Bound light? Bound—or folded?Is this…a secret mystical message??????? HOW DEEP DOES THIS GO???




