Shape #2: Circular Triangle
They're a real thing.
Take three circles and smoosh them close until they’re all touching—tada, you’ve made a circular triangle. Circular triangles are the Shape of the Week. Congrats to circular triangles, long may you reign (for a week)!
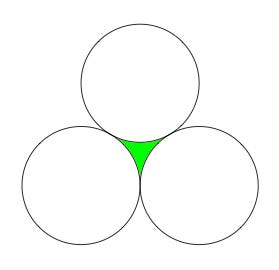
More specifically, the Shape of the Week is the circular horn triangle, which means all its corners are incredibly pointy and its sides are concave (i.e. “all internal angles equal to zero”). If you connect the vertices with circular arcs in different ways you get different circular triangles. But having spent a few days playing around, I can say with some confidence—stick with the horn. It’s the most fun of the bunch.
When I showed this to my students, the first thing they wanted to know was whether all three sides (“sides”) of the circular triangle are always the same length. I told them that I had only known about the existence of these things for about 10 minutes before class started, but that I was pretty confident that the arc-sides could be different lengths. I wanted to quickly whip up a circular triangle on the computer to show them, but I quickly got stuck—I wasn’t sure how to do it.
So, there’s a question: if you draw three points, there’s only one way to connect them with lines. Is there just one way to connect them with circular arcs?
Far be it from me to take away your fun in exploring this! But…
…the answer is “yeah, there’s just one way to do this.” Still, how? To make this more precise, here are two questions:
Given three points, how do you construct all three circular arcs?
Given three points and the distances between them, what should the radius of each circle be?
The first is a geometry question, the second is an algebra question. There are satisfying answers to both. Tell me if you want an answer in the comments.
There is not a lot of information about circular triangles that I could find online, but I did find a 1944 paper by Edward Kasner and Aida Kalish. It begins:
The fundamental ideas for this paper arose during Professor Kasner's lectures in a kindergarten where the youngsters, one day, covered the floor with a thousand tangent, non-overlapping pennies. From this general notion of the packing of coins, the study of the "gaps" or circular horn triangles formed by packing circles in the plane began.
Delightful, and the names rang a bell. After a moment I remembered that this is the same Edward Kasner whose nephew invented “googol.” Very nice! But what did have to say about our Shape of the Week?
The paper consists of a list of theorems concerning the circular (horn) triangles, many of which (this is nice!) totally match the situation with normal, straight-edged triangles. Here are the ones that I understand at this moment:
In a normal triangle, all the perpendicular bisectors meet at a single point. Ditto for the circular horn triangle.
In a normal triangle, the altitudes all meet at a single point. Ditto circular horn triangle!
In a normal triangle, the angle bisectors meet at a single point. It’s not so obvious how you should define “angle bisector” for these strange, circular angles. But the authors do, and guess what? They all meet at a single point, and it looks like this:
“The angle bisectors intersect each other at K at angles of 120 degrees. They are also orthogonal to the given circles opposite the bisected angle.” Sweet.
My last, most recent bit of fun was after I figured out how to make these things on Geogebra. (Here’s my figure.) Drag the points around and you can make all sorts of other circular triangles, but move the dots too far and you suddenly find yourself having created weird, monstrous circular things:
I found a paper that calls these “piecewise circular curves” and while I haven’t read any of the words in that paper, I did quickly skim for the pictures. Figure 6 is nice.
Well, what next? There’s plenty that I don’t understand in both of these papers. And I’m thinking of pulling together some circumference questions involving these circular triangles for my students, since circumference and arc length is our current focus.
But that’s it for now. Tomorrow is another day, next week will feature some other shape, but for now we have circular triangles, another weird shape to add to our growing collection of geometric ephemera. Enjoy!
Update 3/23/23: Great question from class: how many different circular triangles are there for any given three points? (There’s only one circular horn triangle.)
Also another good question: does a circle count as a circular triangle?
I tried linking the points of an equilateral triangle with arc (using OnShape, which is the program I know for playing with geometry...), and it *seems* like I can get three circular arcs happening that aren't equal. Are they secretly overlapping a tiny tiny bit if they aren't all mutually tangent? Or something? (Took a screenshot but can't link it in the comments...)