"Understanding" Shouldn't Be Vague or Mysterious

Let's do some pedagogy.

EdReports, which describes itself as “Consumer Reports for school materials,” has rejected five different editions of Big Ideas Math textbooks, partly for failing to “develop conceptual understanding.” Meanwhile other curricula, like i-Ready, got perfect scores in part thanks to their treatment of “conceptual understanding.”

But what is conceptual understanding, and how do you develop it?

According to their documents, EdReports checks to see if texts include “brief conceptual problems with low computational difficulty,” for example:

• 11 + 6 = ___ + 2

• Find a number greater than 3/5 and less than .75.

• A fraction divided by a fraction is always/sometimes/never less than the original fraction

Curricula also need activities that focus on “concrete representations.” For example, the 7th Grade review of i-Ready specifically cites the following question in their glowing evaluation:

Neva plays a video game. On her first turn, she earns 3 points. On her second turn, she loses 3 points. The expression 3 + (-3) represents her score after the two turns. You can use integer chips to find the sum of 3 and -3.

a. The sum of any number and its opposite is 0. Another term for opposites is additive inverses. Since the sum of 1 and -1 is 0, 1 and -1 form a zero pair. Circle the zero pairs in the model.

b. How many points does Neva have after her second turn?

c. What is 3 + (-3)?

Alright.

The Big Ideas books apparently lack these wordy questions about semi-physical objects. And EdReports complains that in Big Ideas the “conceptual” questions (whatever those are) mainly arrive at the beginning of the lessons, whereas the practice questions are “primarily procedural.”

What does that mean?

EdReports cites all sorts of documents and rubrics. Some of these documents define conceptual understanding, others don’t, and sometimes the definitions clash. This is exactly what researchers Crooks and Alibali found when they reviewed academic papers (about a hundred) for definitions of conceptual knowledge—that “explicit definitions of conceptual knowledge are rare” and “often vague.”

With EdReports we have a relatively clear definition of conceptual understanding but…it’s not great. That video game question isn’t going to help students understand anything. And I have no idea what a “conceptual question” is. Conceptual questions are questions that…develop conceptual understanding? Augh! We’ve gone in a circle.

From iReady. It’s conceptual because eggs.

Fortunately, I think there’s a perfectly sensible definition of conceptual understanding. It’s precise with clear implications for teachers.

It goes like this: conceptual understanding is knowing true and useful generalizations about mathematics. Crooks and Alibali, along with other researchers, sometimes call these principles instead of generalizations, but it’s the same deal—we want students to know facts that apply to a wide variety of cases.¹

Take something like 6 x 3, which kids often think of as six 3s. We might teach kids that 6 x 3 is the same as 3 x 6, so three 6s, which can help them complete the multiplication. Terrific! But we should be more ambitious. We should teach a generally true principle—you can always reverse the order when multiplying—so that they can apply that to any problem, even one like 200 x 3.

I find this an extremely useful guiding classroom principle—to always push for generalizations, facts that are always true. To illustrate, here a few ways this has cropped up in my recent teaching.

“Procedural” Practice Can Develop General Principles

The basic idea of combining like terms is fairly simple—we can always add/subtract like terms as we do numbers—but it needs to be applied in a huge variety of cases. The variety is the challenge.

Obviously there is a limit to how much you can gain from repetitive practice of only one case. But if practice carefully escalates while gradually adding new twists, you give students a chance to apply the general principle to disparate cases.

From Big Ideas, 7th Grade.

This only works if a clear principle has been articulated before the practice. If you do that, though, this kind of practice gives that generalization a workout.

The Teacher Can Articulate the Principle

There’s a sort of discovery-ish vibe associated with conceptual understanding. But there’s no reason that generally useful principles need to be invented by students.

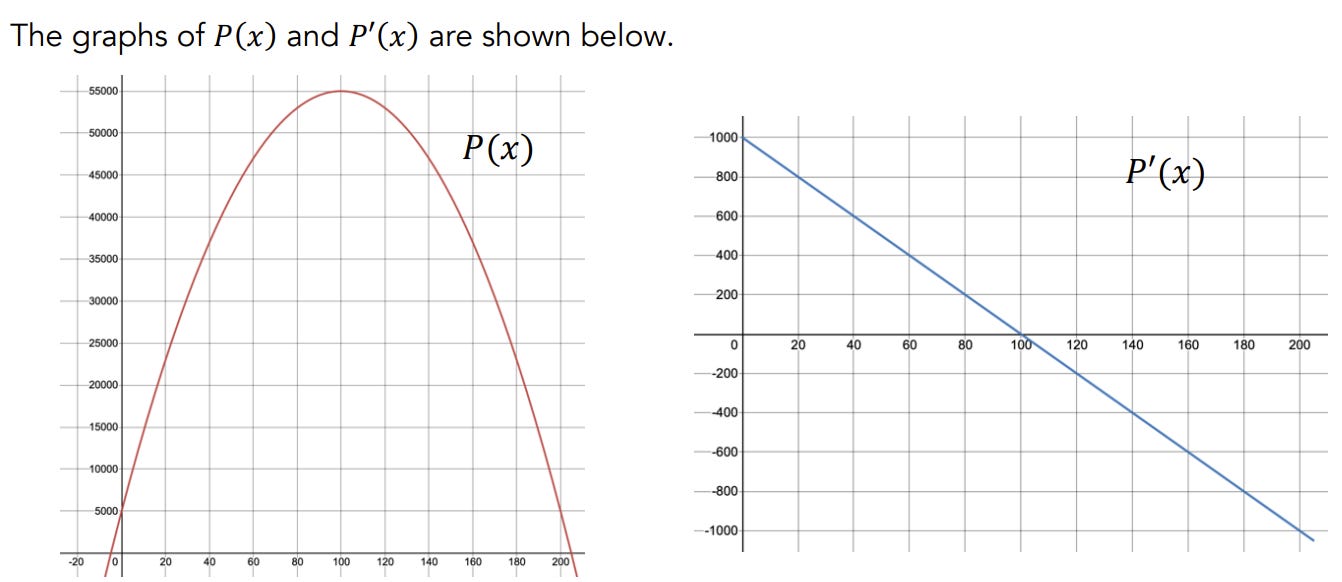
I shared this pair of graphs (from Math Medic) of a function and its derivative in calculus today. (If you’re rusty on calc: the derivative graphs a function’s slopes.) Can you tell, from looking only at the derivative, where the original function is increasing? My students were all able to answer accurately that it’s the portion of the derivative that’s above 0.

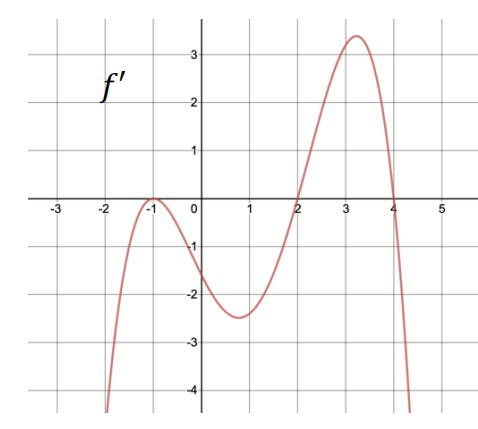
Terrific. But when handed this graph a new derivative they weren’t able to find where the original was increasing.

It was my role to take a step back and articulate the generalization even more clearly. The principle is where the height of the derivative is positive, the function is increasing. “Is the function positive here? How about here?” I pointed at specific points of the derivative. After this students were able to tackle the question. They extended it in the natural way to negative values too. It was good that I said this directly after they got stuck—I wish I’d done it before then.

I sometimes think of this kind of teaching as a generalizing triangle. It’s a pattern that comes up often: teacher talk bumps up the abstraction and students connect it to new particulars.

Correct Explanations are Not Enough

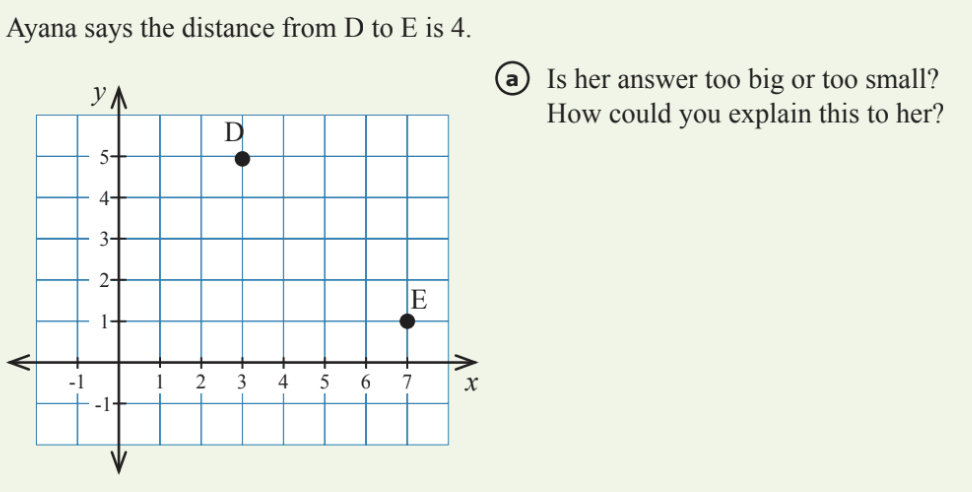
Here is a good question from Transition to Algebra:

When I asked my 7th Graders to answer this, one student pointed out 100% correctly that since it’s four units up from E to D, the diagonal has to be longer than that.

I was about to move on, when I caught myself. I turned back to the kid. “So is the diagonal always going to be more than the vertical distance? Why would that be?”

I’m glad I pushed, because my students responded with two smart generally true answers:

• Yes, the diagonal is always longer than the horizontal or vertical distance, because when going diagonally you’re going in two directions, not just one.

• The Pythagorean Theorem says where the diagonal length is found by adding the squares of the horizontal and vertical distances, and that’s always going to be longer than just the vertical distance squared.

The point of an explanation isn’t just to eliminate doubt—it’s about connecting this particular situation to some generally true fact about the mathematical world.

Visuals are Only Good if They Suggest Principles

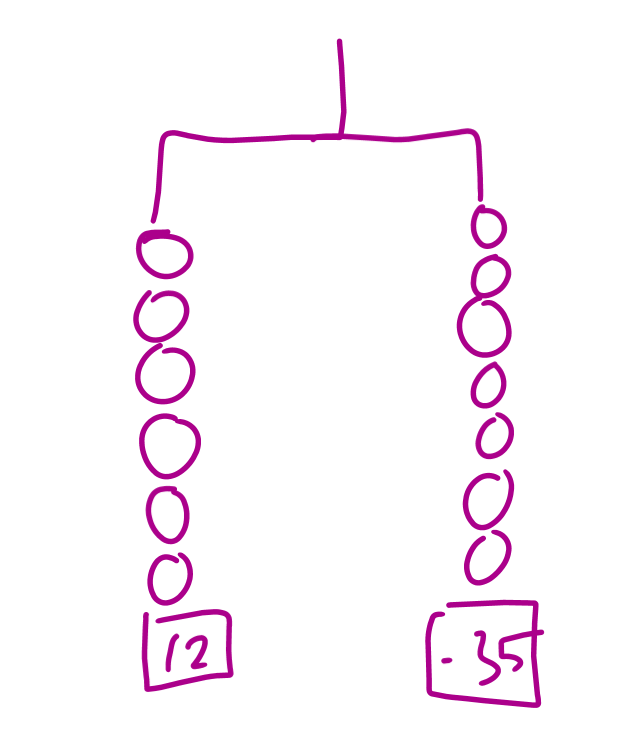
I was explaining to a student how to handle the equation 12 + 6x = 7x - 35. We had talked previously about mobiles, so I drew a quick picture:

“Maybe the -35 is like helium or anti-gravity or something.”

This is a useful move because it’s easy to use the mobile to come up with a true principle—you can remove equal things from both sides of a balanced equation. Our physical knowledge of balance and symmetry are to thank. But that’s only useful if you then leverage that into a true principle about equations, something abstract we have much less experience with. And you have to get rid of the mobile! Its job is to suggest a generalization, then leave.

That integer chip thing earlier…what’s the principle? What are they getting at? Why do they get credit just for using a representation? What is the point of checking to see if textbooks do that?

***

And what about how this all feels, for a student?

Possibly my most frustrating school experience was a semester of Ancient Greek I took in college. Tos theos…I was seriously unprepared. Everyone else in the class had taken either Latin or Greek before; my grasp of English grammar is still on the shaky side. There were rules to memorize but it all felt random, isolated, disconnected to anything else I knew.

I was working with a young student recently on subtraction with borrowing. I’d show him how you could cross out the four and turn it into a fourteen by regrouping. The next question he’d cross out an eight and turn that into fourteen also. It was like that for twenty frustrating minutes. I was failing to help him see the general principle. How frustrating for him! Each subtraction was a brand new problem, unrelated to the one before.

But when it finally clicked…

We all want generalization. We want to see how it all fits together. We want to know how a particular idea flows from something bigger. We want to know how to do things—we also want to know things. We want the whole picture. And when we get it—whether we land on it on our own or someone makes us think of it with words or a picture or anything else—the feeling is terrific, like it all finally makes sense.

1. Crooks and Alibali distinguish between general abstract principles and principles that support procedures. I’m going to ignore that difference.