Shape #10: Orthodiagonal Quadrilateral
Read to the end for classroom questions.
This project has been guided by a single principle, which is that shapes that have dumb names are usually also cool. This is the ironclad law (Pershan’s law) that has helped us land on “sphericon” and “double bubble.”
And yet, today, I am prepared to violate my own precious principle for a shape with a name that you could best describe as “descriptive.” It’s the orthodiagonal quadrilateral, and everything but its name is awesome.
You’ve heard of squares and kites. You’ve heard of rhombuses. In those three shapes, the diagonals are perpendicular to each other, and that’s what defines the straightforwardly-but-inelgantly named orthodiagonal quadrilaterals.
Orthodiagonal quadrilaterals have a number of interesting properties, the first is this: they have a VERY simple area formula. To find the area you multiply the diagonals, and then cut them in half. THAT’S IT.
The proof of this comes very quickly from chopping up these shapes—the orthodiagonal quadrilateral, I mean—into two triangles. And it works like a charm, even in the concave case.
The second really, really interesting property of these shapes is that they have their own special Pythagorean Theorem. This is cheating a little bit because this isn’t really a new Pythagorean Theorem. It’s just the old familiar Pythag put together in a new way, but it’s still very nice, because if the sides of the orthogonal diagonal are labeled a, b, c and d then
Wikipedia has a very nice image for this, basically the sum of the red squares is equal to the sum of the blue squares.
I’m not going to prove it here but Cut The Knot has a very nice proof that doesn’t require a bunch of algebra and can in fact be used to derive the Pythagorean Theorem—if you slide two of the quadrilateral points towards the diagonal intersections, it will get as close to a right triangle as you like, eliminating one of the squares, producing the familiar Pythagorean Theorem. Nifty.
As a total aside, this very much reminds me of a theorem attributed to Jakob Steiner for triangles, the sum of alternating squares around the altitudes are equal. Is there some sort of way to move from Steiner’s result to our orthogonal quad case?
The final property that I’ll mention is that “orthodiagonal quadrilateral” is twenty eight characters long, which is way too long for a shape this nice but what can I say? Orthodiagonal quadrilaterals are the shape of the week, we do what we must.
QUESTIONS THAT MIGHT BE FUN TO ASK STUDENTS
Can you find the area of a square using just the diagonals and this formula? If each side of the square is s, show that this formula and the usual one agree.
Use the proof shown up above to find the area for that concave orthodiagonal quadrilateral.
Connect the midpoints of all those orthodiagonal quadrilaterals up above. What shape do you get? Why is it always that shape?
The area of an orthodiagonal quadrilateral is 24. How long could its diagonals be if it’s a kite? A rhombus? A square?
If you’re following along, I’d love to hear any ideas you have for classroom questions. Chime in!


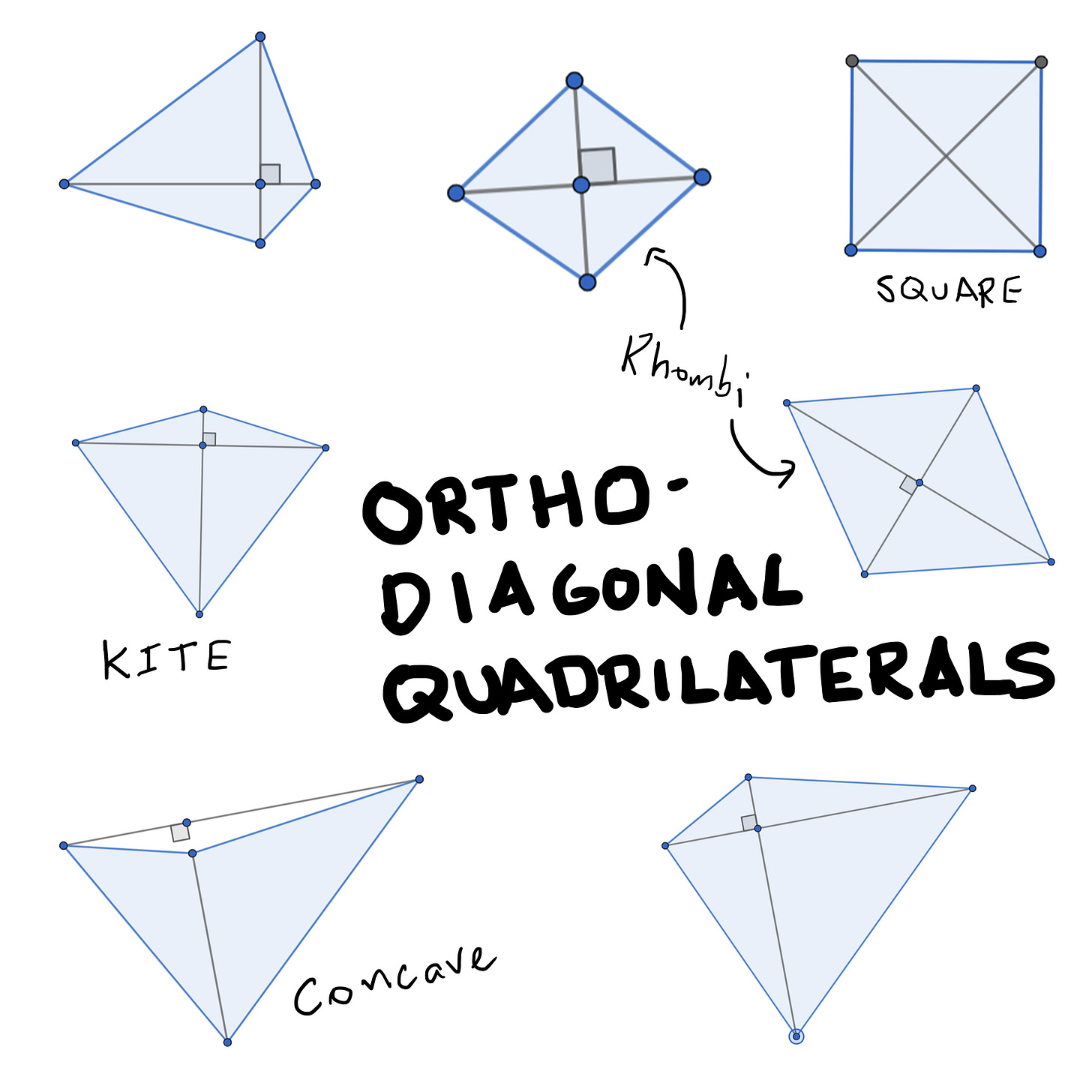

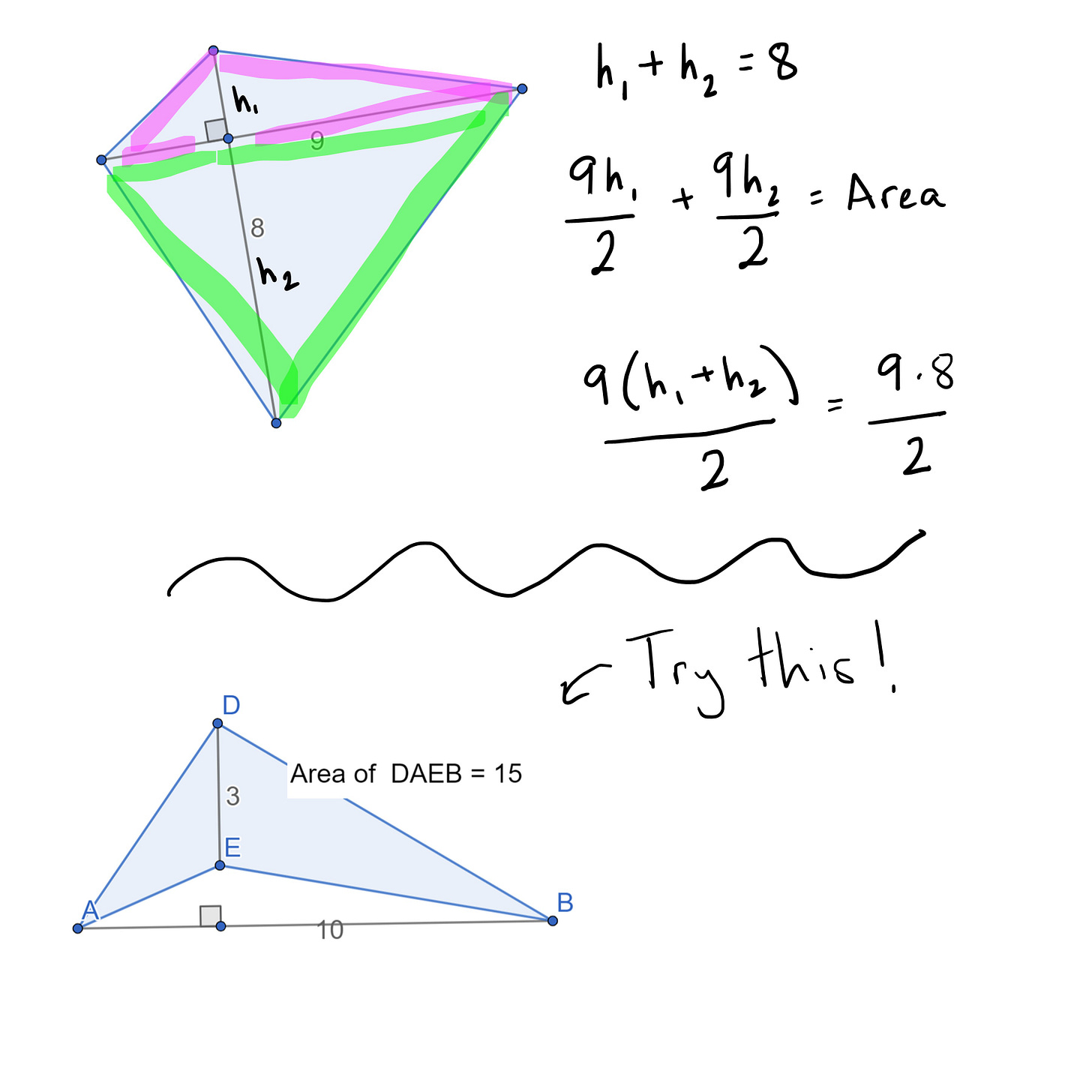


Here's another set of questions you could ask students: What is a more familiar name for an orthodiagonal rectangle? An orthodiagonal parallelogram? Does an orthodiagonal trapezoid have a more familiar name too?