Double Bubbles

It's the shape of the week

I have a weakness for funny-sounding shapes, and to a certain extent this “shape of the week” project is animated by a search for things that are interesting to say. The list of shapes that we’ve chosen so far speaks for itself—zonogons, triangular circles, salinons. Go ahead, say them. You’ll see, it’s fun.

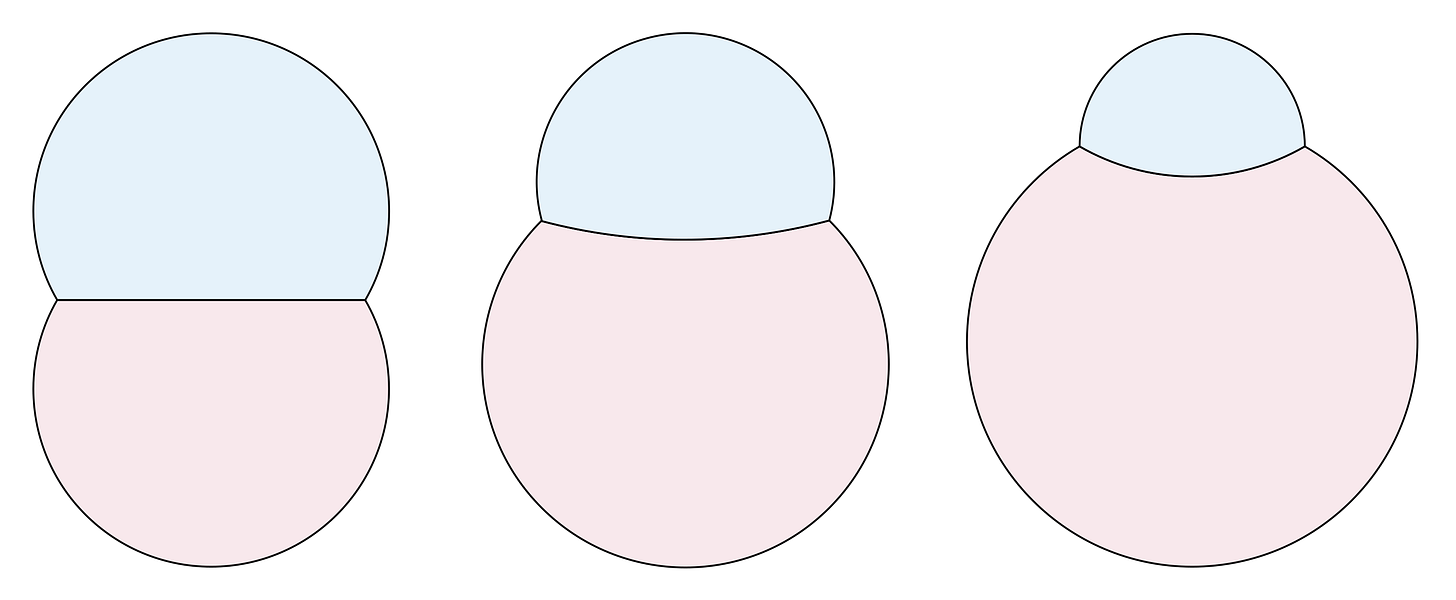
That’s a long way of explaining why the shape of the week this week is the double bubble, a shape that is ten-thousand times more fun to say than “rectangle,” and my colleagues tell me the 2D version looks like a butt.

Some double bubbles from wikipedia. Thanks, wikipedia!

A cool thing about bubbles is that they tend to minimize surface area. If you put a frame in a bunch of bubble solution it’ll form all sorts of interesting films that connect the frame in the least possible surfaces—sometimes in surprising ways. That’s true in three- and two-dimensions.

Photo of matheamtician John Sullivan by Ulrich Dahl in Quanta

So, let’s say you’ve got an acre of crops that you want to fence in, and you want to use as little fencing as you can. What shape should you use? This is called the isoperimetric problem and the answer is the circle.

Now let’s give you two crops to fence in. You want to plant an acre of each, and you do NOT want the crops to come into contact. You’re still a cheapo and you’d prefer to minimize your fencing costs. What should the shape be?

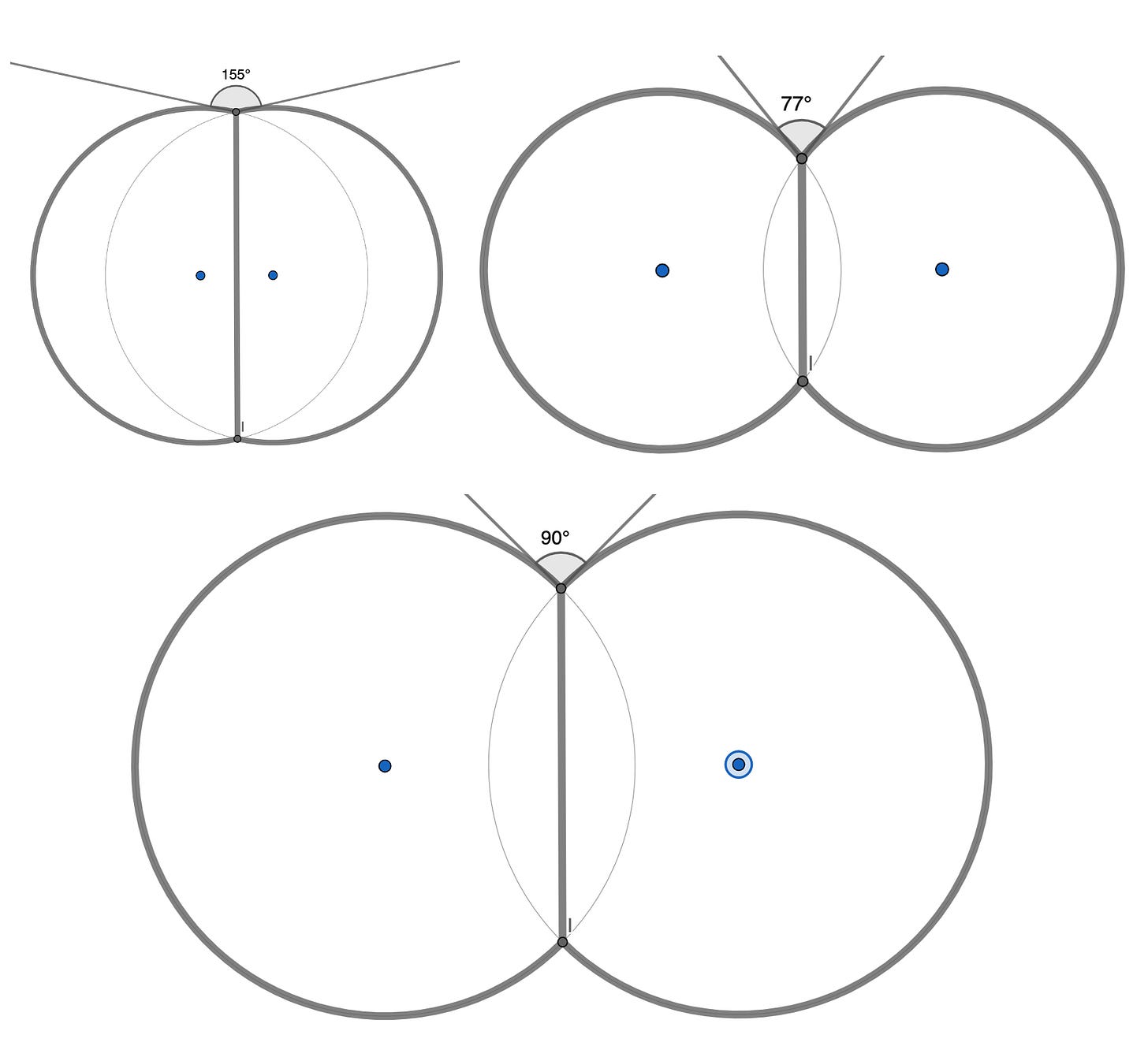
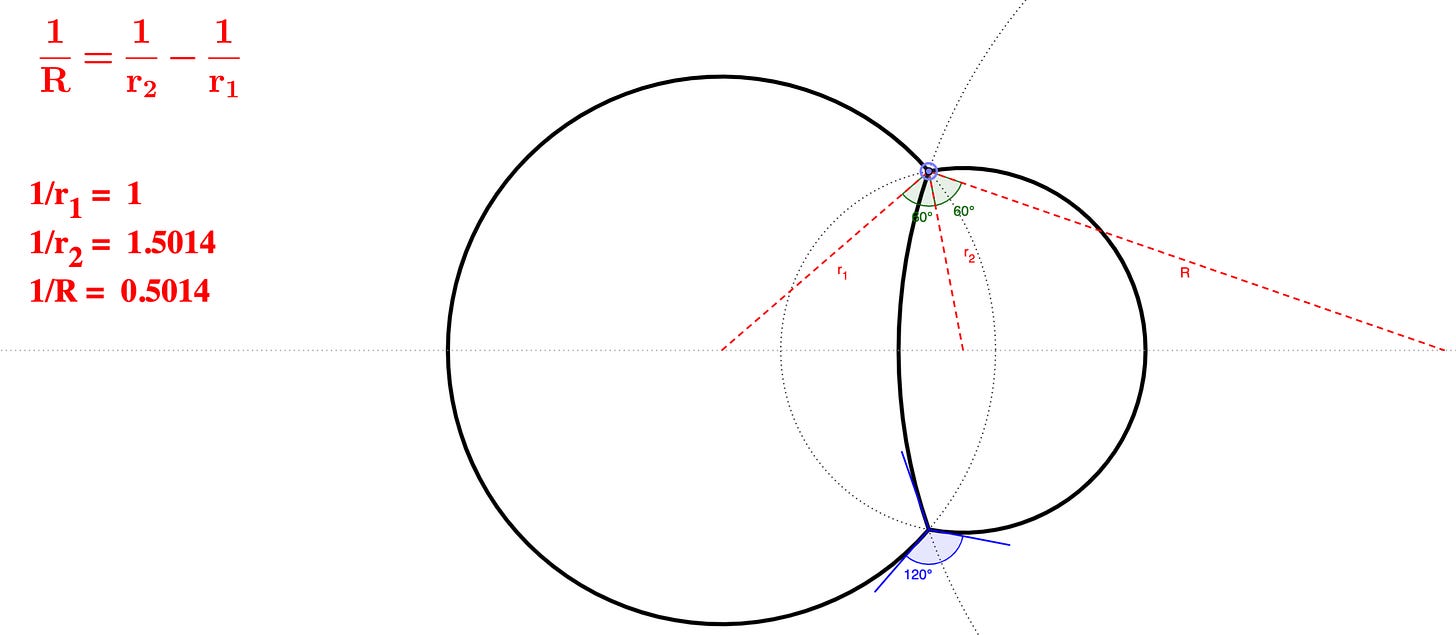
It should be a double bubble, which is made of two big arcs and the boundary between them—hold on, which one? Is it the one where the circles meet at 90 degree angles? Or 155 degrees? Or maybe some other angle between them?

(Small print: we’re drawing tangents to the circles at the point of intersection. Play with it in geogebra here. But that’s cool—we can find angles between curves now!)

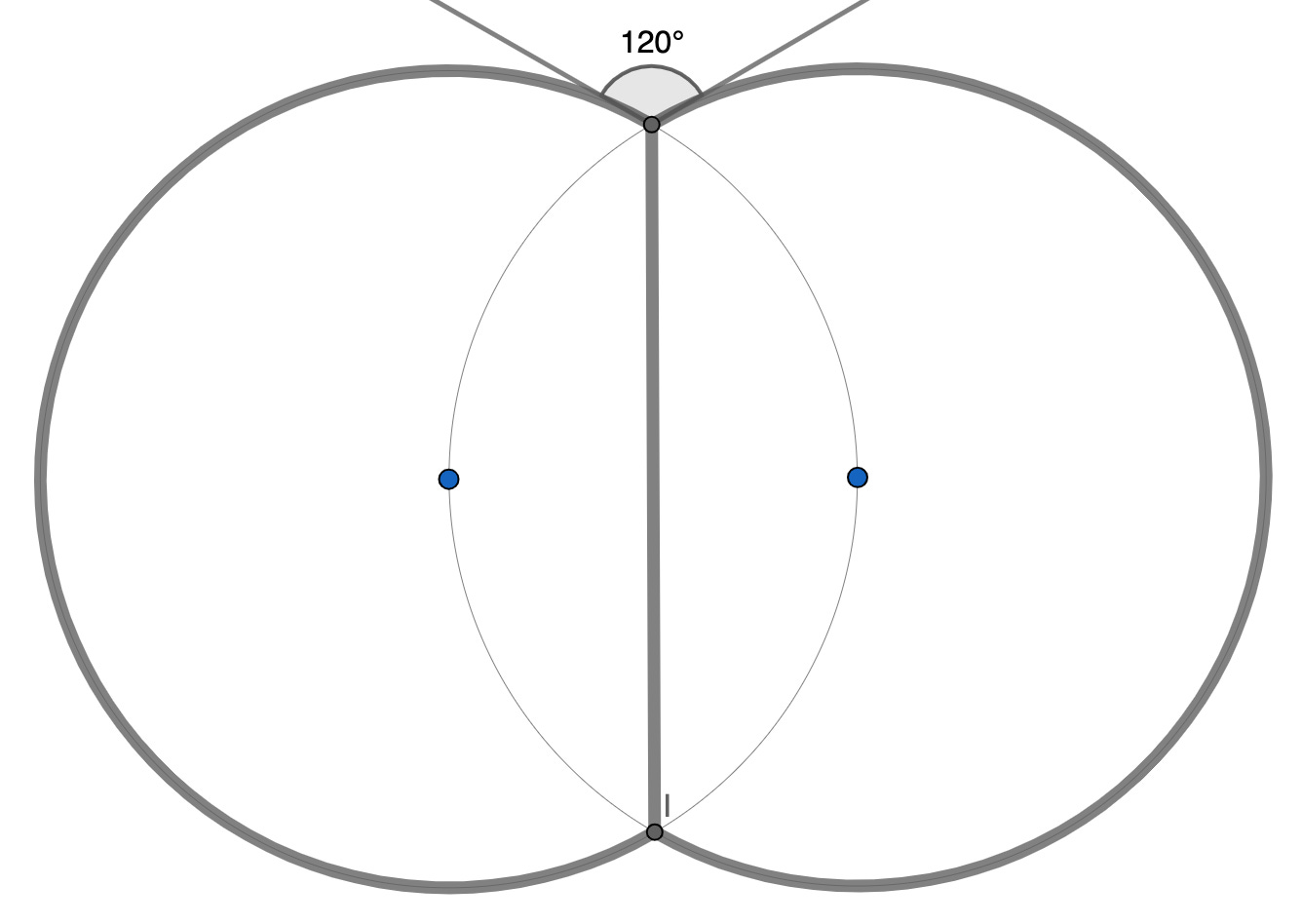
This is a question that has an answer: the bubbles need to intersect at precisely an 120 degree angle, and this is called the standard double bubble. It minimizes the perimeter, given the two areas.

It does sort of look like a butt.

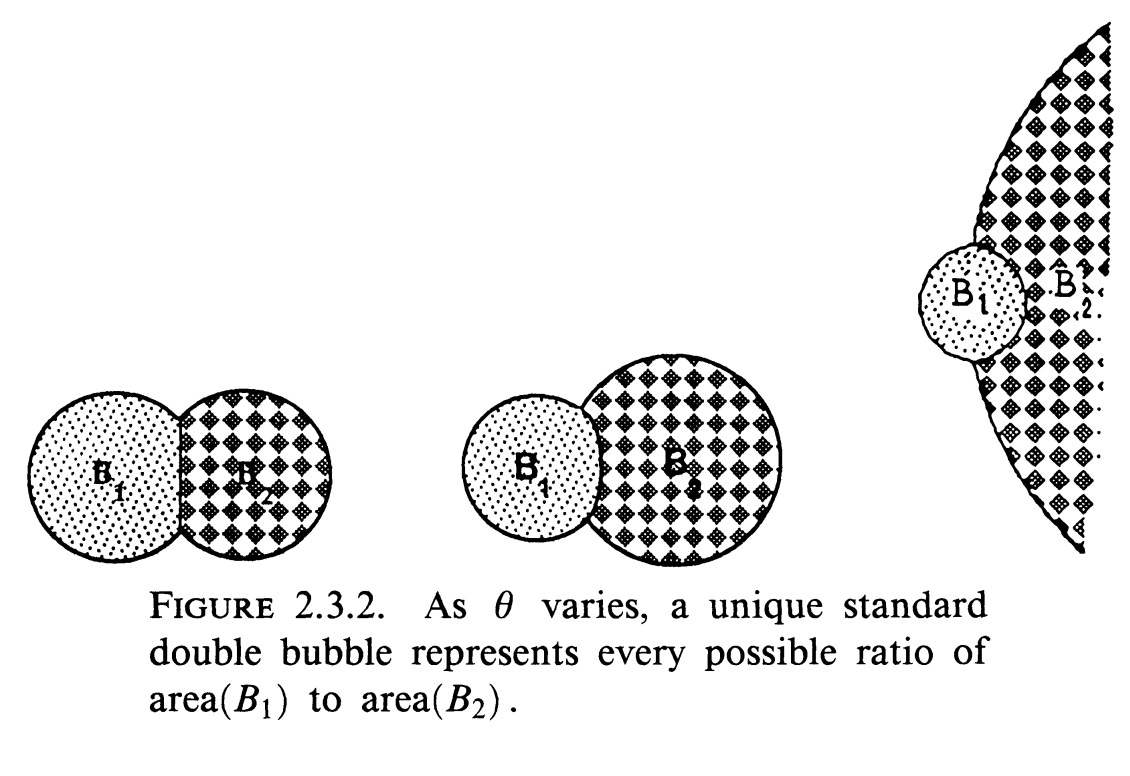
Another twist! What if the areas we’re trying to enclose aren’t the same? What if we have 5 acres of wheat and 2 acres of corn, and we want to fence them in with as little fencing as possible? Is it still a double bubble?

And the answer is heck yeah it is! Though now the boundary is itself a circular arc, not a line. It even sort of ends up looking like a 3D bubble. I have very much enjoyed playing around with this geogebra applet from Karl-Otto Markussen and I’m betting you will too.

It took me a while to try to get even a basic understanding of this arrangement. Why doesn’t the line straight down minimize the areas—why does it have to be an arc?

But the problem is (apparently) that to minimize the perimeter we need THREE angles of 120 degrees. When the circles aren’t the same size, a dashed line straight down doesn’t cut the remaining 240 degrees in half evenly. We need a third arc to connect those points and divide the areas.

No dice.

Now, that all this stuff minimizes perimeter is apparently hard to prove, which is why it took a very long time to do. The 2D version was shown in 1993 by a bunch of undergrads (which included Jason Zimba), and they wrote a paper that I’ve been poking around in this week.

From their paper.

But there were all sorts of open questions—what about the 3D version? Does the triple bubble minimize perimeters for three areas? Four? Five? What about higher dimensions? Just last year many of these problems were finally solved—though not them all.

Whatever—I’m still into these 2D double bubbles. As a little extra assignment, I asked students to find the area of a few of these double bubbles, which is not necessarily easy for kids.

And there’s one more fun thing, which is that there are three circular arcs in the double bubble, all with their own radius. There’s the two bubbly-looking circles, plus the part of a circle between them. Is there any connection between all these radii?

The answer is yeah! Though I don’t yet really know how to derive the relationship.

So, hooray for double bubbles. They sound fun, look like butts, and have all sorts of interesting geometrical properties.

Assorted Other Links:

• A nice intro to bubble math at Brilliant.org.

• A compass-and-straightedge construction of the double bubble.